PI Acaba? Vincenzo Bongiovanni Renate Watanabe         Introdução Não, "não acaba" - e o interesse que ele desperta também parece não acabar. Já se falava do número há cerca de 4 000 anos. Vamos, neste artigo, contar alguns trechos da longa história do número . Ela será dividida em 4 períodos (nem sempre disjuntos). Os períodos vão se diferenciar pelos métodos usados na determinação de , pelos objetivos imediatos do cálculo e pelas ferramentas matemáticas então disponíveis.        Primeiro período [10] E o período "geométrico" e vai desde as primeiras estimativas da razão entre o comprimento de uma circunferência e o seu diâmetro até o surgimento do Cálculo, em meados do século 17. O objetivo era encontrar uma expressão racional para e as principais ferramentas, o princípio de exaustão e a determinação de perímetros e áreas de polígonos regulares inscritos e circunscritos a uma circunferência. Os primeiros vestígios de uma estimativa de encontram-se no Papiro de Rhind (RPM 15, p. 18) escrito, aproximadamente, em 1700 a.C, onde se lê: a área de um círculo é igual a de um quadrado cujo lado é o diâmetro do círculo diminuído de sua nona parte. Acredita-se que este resultado tenha sido obtido empiricamente.   Os babilónios atribuíram a o valor 3 e, em outros escritos, 25/8. No Velho Testamento (1 Reis VII, 23 e 2 Crônicas IV, 2), bem como no Talmud, — 3. O primeiro resultado científico e notável foi obtido por Arquimedes (287-212 a.C.) usando o método de exaustão, descrito no livro 10 de Euclides: Dadas duas grandezas distintas,  se da maior subtrairmos uma grandeza, maior do que sua metade e do que restar,  uma grandeza maior do que sua metade, e se este processo for repelido  continuamente, restará alguma grandeza menor do que a menor das duas grandezas iniciais. (Usando este princípio, os gregos conseguiram resolver diversos problemas envolvendo o que hoje chamamos de "limite".) Arquimedes partiu de um hexágono regular e calculou os perímetros e áreas de polígonos regulares de 6, 12, 24, 48 e 96 lados, inscritos e circunscritos a uma circunferência e mostrou que (Para melhor apreciar este resultado, observe que ele equivale a dizer que está entre 3,14084 e 3,14285 e foi obtido numa época em que não havia nenhuma notação conveniente tais aproximações.) O método de Arquimedes foi usado pelos séculos afora e nenhum método significativamente melhor para a determinação de foi encontrado até o advento do Cálculo. Para se ter unia idéia da universalidade do cálculo de , citaremos alguns nomes e datas deste primeiro período. Ainda na Grécia, Ptolomeu (87-165) calculou as cordas de todos os ângulos de meio em meio grau, entre 0 e 180 graus, e obteve para o valor aproximado 3,14166.   Na índia, Aryabhata ( 500) e, posteriormente, Bhaskara ( 1140) obtiveram para o valor 3927/1250 3,1416, calculando os perímetros de polígonos de 12, 24, 48, 96 e 384 lados. 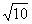Para Brahmagupta ( 628), = Na China, no século 12 a.C, o valor de era 3 e, no início da era cristã,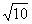. Tsu Ch'ung-chih (430-501) obteve para o valor 355/113 ( 3,1415929), valor este redescoberto na Europa 1000 anos depois [3]. Nos séculos 15 e 16, com o desenvolvimento da trigonometria e uma notação melhor para números, a determinação dos comprimentos de cordas tornou-se mais precisa e mais rápida. Matemáticos desta época, ainda usando o método de Arquimedes, calcularam com até 35 casas decimais. Uma idéia nova foi usada por Descartes (v. p. 9). Ao invés de considerar, numa mesma circunferência, polígonos inscritos e circunscritos com um número cada vez maior de lados, Descartes fixou o perímetro dos polígonos e calculou os raios das circunferências inscrita e circunscrita. Começando com um quadrado de perímetro 2, dobrando sucessivamente o número de lados dos polígonos e mantendo fixo o perímetro, é fácil mostrar que a seqüência dos raios das circunferências inscritas (e também a dos raios das circunferências circunscritas) tende a  l /.  O método usado por Descartes é conhecido como o método dos isoperímetros e pode ser encontrado em [9], pp.  177-181. Cumpre lembrar que as dificuldades no cálculo de sempre foram de natureza computacional, não conceitual. 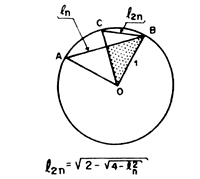Usando tão-somente o teorema de Pitágoras, é possível obter (teoricamente) aproximações tão precisas de quanto forem desejáveis.  Basta relacionar o lado de um polígono de 2n lados com um de n lados, ambos inseridos na mesma circunferência, para poder calcular os perímetros de polígonos com um número muito grande de lados.        Segundo período [12] Os resultados do primeiro período foram, de certo modo, decepcionantes. Esperava-se que , relacionado com a mais perfeita das formas geométricas, fosse um número muito especial  e o fato de não se ter encontrado uma expressão especial para parecia indicar que o seu segredo não fora ainda desvendado. No século 17, com o advento do Cálculo, a determinação de ganhou novas e poderosas ferramentas, que substituíram os métodos geométricos até então usados. 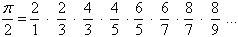Um resultado inicial foi publicado por John Wallis em 1655: (ver em [3], p. 281, como chegar a este resutado). 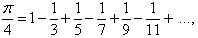Neste período, a série mais usada no cálculo de  foi a série de Gregory, publicada em 1670 : Para  x = 1, obtém-se resultado este obtido independentemente por Leibniz e publicado em 1674. Esta série, por convergir muito lentamente, não é adequada para o cálculo de , mas, sob o ponto de vista estético, atende bem ao sonho daqueles que buscavam uma representação especial para . Daí para frente, com a série de Gregory e algumas relações trigonométricas, cada vez mais casas decimais de foram calculadas e em tempos cada vez menores. 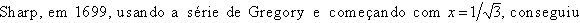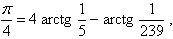Eis alguns exemplos: obter 72 casas decimais de Machin, em 1706, usando a mesma série e a identidade conseguiu calcular com 100 casas decimais. (É fácil ver por que o uso desta identidade facilita o cálculo de . Ela nos diz Os cálculos no primeiro parêntese podem ser simplificados substituindo 1/5 por 2/10 e a série no segundo parêntese converge muito rapidamente.) Euler, em 1755, usando outras relações trigonométricas, obteve uma série rapidamente convergente, o que lhe permitiu calcular as primeiras 20 casas decimais de em uma hora. Dase, um calculador prodígio, em 1844, calculou com 200 casas decimais, em menos de 2 meses. (Por recomendação de Gauss, Dase foi contratado pela Academia de Ciências de Hamburgo para determinar todos os fatores dos números inteiros entre 7 e 10 milhões.) E assim foi, até que ... Shanks, em 1873, usando a fórmula de Machin e após 15 anos de trabalho, obteve com 707 casas decimais (527 corretas).             Terceiro período Este período é caracterizado por dois resultados não ligados ao valor de , mas à sua natureza. Em 1761, Johann Heinrich Lambert demonstrou o seguinte teorema: Se x for um número racional, diferente de 0, então tgx não poderá ser um número racional. Uma consequência 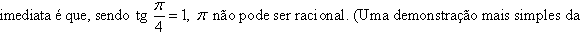irracionalidade de foi publicada, em 1947, por I. Niven e pode ser encontrada em [7].) Mais de 100 anos depois, em 1882, Ferdinand Lindemann provou que é transcendente, ou seja, não é raiz de nenhum polinômio com coeficientes racionais [7]. Este último resultado resolveu o famoso problema da quadratura do círculo que vinha desde a antiguidade. O fato de ser transcendente prova, definitivamente, ser impossível construir, somente com régua não graduada e compasso, um quadrado e um círculo de mesma área.   é irracional, é transcendente e havia sido calculado com 707 casas decimais. A sua história talvez tivesse chegado ao fim se não fossem os computadores.        Quarto período [6] Em 1949 o interesse pelo número havia ressurgido. Por um lado, os computadores permitiam a determinação de um grande número de casas decimais de e, por outro, foram levantadas algumas questões interessantes quanto à distribuição dos algarismos de . Por exemplo, Emile Borel (1871-1956) perguntou se era um número "normal", isto é, se na sua representação decimal cada algarismo ou grupo de algarismos aparecia com a mesma freqüência. (Conjetura-se que a resposta seja afirmativa, mas o fato ainda não foi demonstrado.) Ou, se seria possível, algum dia, calcular o n-ésimo dígito de sem calcular os n 1 dígitos anteriores. O primeiro cálculo de , por computador, foi feito em 1949, produzindo 2 036 casas decimais em 70 horas/máquina. Mais recentemente (1988?), D. H. Bailey obteve com mais de 29 milhões de algarismos em 28 horas/máquina [1]. A revista Science News, de setembro de 1989, noticia que David e Gregory Chudnoviski calcularam com 1 bilhão de algarismos decimais exatos. Embora o cálculo de com milhares de casa decimais tenha sido usado para testar computadores novos e treinar seus usuários, ele certamente não é trivial. Requer fórmulas eficientes, programas bem escritos e vários esquemas que permitam economizar tempo e espaço na memória do computador. Alguns desses cálculos usam a série de Gregory e relações trigonométricas do tipo Mais recentemente, entrou em uso um método iterativo baseado na média aritmética-geométrica, estudada por Gauss em volta de 1800 [1]. Esta média foi usada, pela primeira vez, na determinação de , por Tamura e Kanada, em 1981 (ao calcularem com 4 milhões de casas decimais) e, por causa de sua rápida convergência, tem, hoje em dia, um papel muito importante na computação.   Nessa mesma linha, J. M. Borwein e P. B. Borwein [8], por volta de 1984, obtiveram um algoritmo que permite calcular com uma precisão e velocidade impressionantes. O algoritmo y0 = 0 , 0 = 2 e pelas fórmulas de iteração:   A convergência de   n+ 1    para      é muito rápida:  com  4  passos obtém-se 4 = 3,14159 26535 8976 E + 000 ou seja, o valor de com 14 casas decimais corretas! A história, por enquanto, termina aqui.  Mas fica a pergunta: haverá, algum dia, um quinto período na história de ?   Referências Bibliográficas [1]   Almkvist, G. e Berndt, B. "Gauss, Landen, Ramanujan, the aritmetic-geometric mean, ellipses, , and the Ladies Diary". The American Mathematical Monthly, agosto-setembro, 1988, pp. 585-608. [2]   von Baravalle, H. "The number " em Historical Topics for the Mathematics  Classroom, NCTM, 1969, pp. 148-154. [3]    Boyer, Carl B. História da Matemática. São Paulo, Editora Edgard Blucher, 1974. [4]    Costa, Roberto C. F. "O que é um número transcendente?". RPM 1, 1982, pp. 14-15. [5]    Davis, Philip J. The Lore of  Large Numbers. New York, Random House, Inc., 1961. [6]    -------- ., Chinn, W. G. 3,1416 And AH TJiat. Boston, Birkhãuser, 1985, pp. 172-180. [7]    Figueiredo, Djairo G. Números Irracionais e Transcendentes, capítulos 3 e 7. Rio de Janeiro, SBM, 1980. [8]    Flanders, Harley.   "Computing ".   The College Mathematics Journal, vol. 18, n. 3, maio 1987, p. 230. [9]    Hadamard, Jacques.   Leçons de Géométrie Élémentaire, v.   1.   Librairie Armand Colin, Paris, 1911. [10] Hobson, E. W. Squaring The Circle. Cambridge, 1913; reimpressão: New York, Cheslea Publishing Company, 1953. [11]  Lima, Elon L. "O que é o numero ?". RPM 6, 1985, pp. 18-20. [12] Wrench Jr., J. W. "The evolution of extended decimal approximations to ".  The Mathematics Teacher,   dezembro, 1960, pp. 644-650.   Calculadores de   decimais tempo Ptolomeu, 150 4   Viète, F., 1579 10   Romanus, A., 1593 16   van Ceulen, L., 1610 35   Sharp, A, 1699 72   Machin, J., 1706 101   Dase, Z., 1844 201 2   meses Shanks, W, 1873 707 15  anos ENIAC em Aberdeen, 1949 2036 70  horas NORC em New York, 1954 3093 13 minutos Genuys, F.1959 10 000 l h40m Shanks, D. e Wrench Jr., J. W., 1961 100 000 8h43m Gilloud, J. e Dichampt M., 1967 500 000 44h45m Gilloud, J. e Bouyer, M., 1976 1000 000   Tamura, Y e Kanada, Y, 1982 4194 293 2h53m Tamura, Y e Kanada, Y, 1988 16 000 000   Chudnoviski, D. e G., 1989 1 bilhão     Vincenzo Bongiovanni é licenciado em Matemática pelo Instituto de Matemática e Estatística da USP e mestre em Matemática pela PUC-SP. Leciona no Colégio Universitas e na Universidade de Santos e é co-autor da coleção "Matemática e Vida" da Editora Ática.