José Paulo Quinhões Carneiro
Rio de Janeiro, RJ

Tenho o triplo da idade que tu tinhas quando eu tinha a idade que tu tens. Quando tu tiveres a idade que eu tenho, teremos juntos 56 anos. Qual é a minha idade?

Este problema, hoje meio fora de moda, foi célebre numa época em que havia uma preocupação de resolver este e outros tipos de problemas "por Aritmética" e não "por Álgebra". Tenho observado que, no âmbito escolar, este problema causa uma espécie de terror, enquanto fora dele exerce até um fascínio sobre as pessoas, talvez pelo seu enunciado exótico, em estilo de uma charada.

Vamos abordar o problema geometricamente. Se representarmos graficamente, num sistema de 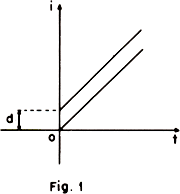coordenadas cartesianas, a evolução da idade de um indivíduo através do tempo, obteremos sempre uma reta paralela à bissetriz do primeiro quadrante. Na realidade, obteremos a própria bissetriz se tomarmos o "ano zero" como sendo o ano de seu nascimento, pois no ano 1 ele terá 1 ano, e assim sucessivamente (isto é um fato do qual a experiência já mostrou que podemos convencer mesmo uma pessoa que jamais estudou Geometria Analítica).Já a idade de uma pessoa  d anos mais velha terá como gráfico uma reta paralela, já que a diferença entre as idades dos dois permanecerá constante e igual a d (fig. 1).

Voltemos então ao nosso problema. Há dois indivíduos em causa, um que fala (chamamo-lo de E) e um que escuta (T). Evidentemente E é mais velho que T (... quando eu tinha a idade que tu tens ...), digamos, d anos, de modo que seus gráficos de idades se assemelham aos da fig. 1.

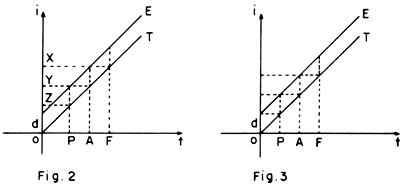
Há três épocas mencionadas no problema, que chamaremos P (passada), A (atual) e F (futura). A maneira como se relacionam A e P (...quando eu tinha a idade que tu tens...) e a maneira como.se relacionam A e F (... quando tu tiveres a idade que eu tenho ...) mostram que elas se situam no gráfico como na fig. 2.

A inclinação de 45° possuída pelas retas do gráfico acarreta que todos os segmentos assinalados têm comprimento d.

O dado de que a idade que E tem na época A (isto é, OX) é o triplo da idade que T tinha na época P (isto é OZ), juntamente com o fato de XY = YZ = d, obriga a que OZ seja também d (estou evitando escrever a equação 2d + OZ = 3OZ, já que isto pode ser "visto" na figura). Mas, então, a reta gráfica da idade de E tem que passar por Z e a figura correta é a fig. 3.

Agora então é claro que, na época F, a idade de T é 3d enquanto a de E é 3d + d. Logo os dois juntos têm 7d, que deve ser 56. Logo d tem que ser 8 e a "idade que eu tenho"é   3x8=24, que é a resposta.

Para encerrar, gostaria de acrescentar que esta aparente brincadeira pode ter implicações mais sérias. De fato, desde 1875, os demógrafos costumam utilizar o célebre diagrama de Lewis, que nada mais é do que um gráfico idade x tempo, onde exercem um papel básico as linhas de vida (ver, por exemplo, Smith, D.; Keysitz, N. Mathematical Demography , Springer-Verlag,  1977, p.39).   Além disto, as linhas de vida são "curvas características" de uma equação diferencial parcial, fundamental em Demografia, a equação de Von Foerster.

José Paulo Quinhões Carneiro é Doutor em Matemática pela UFRJ. Trabalha como analista e consultor da Fundação IBGE e ê professor de Matemática da UFRJ. Tem vários trabalhos publicados sobre demografia e índices de concentração de renda.