|
Eduardo
Wagner
Num
plano horizontal fazemos três furos em A, B e C e passamos
por eles cabos (sem massa nem espessura) que são amarrados em P. Em
cada uma das extremidades, A', B' e C", prendemos pesos iguais
(k). Não há atrito em A, B e C, é claro.

O
sistema formado pelos três pesos ficará em equilíbrio quando o seu
baricentro estiver o mais baixo possível; a Mecânica nos ensina. A
distância do baricentro do sistema ao plano é

que deve então ser máxima. Mas, como o comprimento total dos cabos é
AA' +
BB' + CC + PA + PB +
PC- constante ,
concluímos que na posição de equilíbrio PA + PB + PC é mínimo! Ora,
em P atuam 3 forças horizontais de igual módulo com resultante
nula. Isto implica que elas fazem ângulo de 120°, duas a duas.
Observações:
1. Se um
dos ângulos do triângulo for maior ou igual a 120°, observaremos o sistema
entrar em equilíbrio quando o nó P estiver no furo correspondente a
este ângulo.
2. Suponha que A, B e C sejam
colégios com populações diferentes e
P seja uma praça de esportes comum. Onde deve se localizar P
para que a soma das distâncias percorridas por todos os alunos desde os
seus colégios até P seja mínima?
Não há
solução elementar conhecida, mas a "solução mecânica"funciona
maravilhosamente. Basta prender em cada fio um peso proporcional à
população da respectiva escola e deixar o sistema entrar em equilíbrio.
NR
: Uma justificativa para a "resolução mecânica"pode ser feita utilizando
cálculo de funções de duas variáveis. Veja o artigo a seguir.
|
Uma busca de soluções para o problema de Steiner |
Sérgio Rodrigues
Uma
generalização natural do problema de Steiner é a procura de um ponto que
minimiza a soma das distâncias a n pontos dados. Mostraremos aqui que
esta busca pode ser reduzida a um conjunto de pontos especiais. O resultado
apresentado dá uma justificativa para a solução mecânica do problema (vista
acima).
 se P
se P
 Ai,
para
i
= 1,2,... ,n.
Ai,
para
i
= 1,2,... ,n.
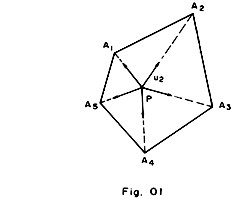 Teorema:
Existe pelo menos um ponto P no plano que minimiza a soma das distâncias
a cada um dos pontos A1,A2,...
,An e se P é um destes pontos então (
i
) ou P é um dos pontos Ai,
(ii) ou
P Teorema:
Existe pelo menos um ponto P no plano que minimiza a soma das distâncias
a cada um dos pontos A1,A2,...
,An e se P é um destes pontos então (
i
) ou P é um dos pontos Ai,
(ii) ou
P
 Ai
para
i = 1,2,... n Ai
para
i = 1,2,... n
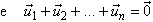
isto
é, P é um ponto de
equilíbrio das "forças"

|
1. O caso n
=
3 e o problema "Onde Morar" |
Pelo
teorema acima, se o ponto P minimiza a soma das distâncias a
A1,A2,A3
e não é um

(1)
Se um dos ângulos do triângulo é
maior que 120°, usando argumentos
de arco capaz, podemos concluir que
não existe um ponto P do plano que
satisfaz (1), donde, pelo Teorema, o
valor de mínimo da soma é atingido
em um dos vértices. Como o maior lado
de um triângulo se opõe ao maior
ângulo, segue que o vértice
correspondente ao maior ângulo é o ponto que
minimiza a soma desejada.
(2)
Se todos os ângulos do triângulo são
menores que 120°, então, por
argumento de arco capaz, existe um
único ponto P interior ao triângulo
A1A2A3
que satisfaz (1). Pelo Teorema, o valor de mínimo desejado para a
soma das distâncias será atingido no ponto P que satisfaz (1) ou
nos vértices
do triângulo.
Considere a seguinte figura:
O
triângulo A1P'A'3
é obtido rodando-se o triângulo
A1PA3
de 60° em torno de A1.
Por argumentos semelhantes aos utilizados no artigo Onde
Morar,
temos que A'3,P',
P, A2
estão alinhados e
A'3A2
= A,P + A3P + A2P < A'3A1
+ A1A2
= A3A1
+ A1A2.
Com isto
concluímos que o vértice Ai não é ponto de mínimo. O mesmo
procedimento aplicado aos demais vértices nos leva à constatação de que o
único ponto de mínimo é P.
Para o leitor familiarizado com
cálculo diferencial, apresentamos um
|
2. Esboço da prova do Teorema no caso
n = 3 |
Sejam
Ai = (ai,bj)
, i =
1,2,3 e Q =
(x,y)
pontos do plano. A distância de Q à Ai é

Tome a
função definida no plano IR2

Por resultados do cálculo diferencial
de duas variáveis temos que

(b)
A função / só não possui derivadas parciais nos pontos Q =
A1,
A2
e A3,
pois a raiz quadrada (2) é zero.

e se calculamos as derivadas parciais
de f
usando (2), temos
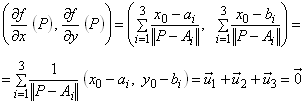
O teorema fica concluído de (a) (b) e
(c).
|
3.
Comentários e Sugestões |
1 - O teorema aqui apresentado não
resolve, em cada caso, qual é o(s) ponto(s)
que minimiza a soma das distâncias mas reduz a procura deste(s) ao conjunto
dos pontos formado pelos vértices e pontos de equilíbrio.
Nem sempre é fácil
determinar quais são os pontos de equilíbrio no caso geral de n
pontos.
2 - Propomos que o leitor
investigue as possíveis soluções para o caso de
n = 4
e
n
=
5
e em que os pontos formam uma linha poligonal convexa.
|
 |
|
Sérgio
Rodrigues é doutor pelo
IMPA, trabalha na área de Sistemas Dinâmicos e é professor na Universidade
Federal de São Carlos. |
|
 |
|