|
Uma nova seção
Atendendo ao
interesse manifestado por vários leitores e por sugestão do
Editor
convidado, João Bosco Pitombeira, este número da RPM inaugura
uma
nova seção da Revista, dedicada, exclusivamente, ao estudo das construções
geométricas.
Esse é um
assunto que, talvez por exageros cometidos pelos seus defensores
mais exaltados ou, ainda, por simples modismo de época, andou meio esquecido
e, agora, começa a ressurgir. Em sua defesa podemos invocar não apenas
o fato de ser ele fonte inesgotável de problemas de todos os graus de dificuldade,
como também o de ser um elemento integrador no estudo da Geometria,
Álgebra e Aritmética. Uma ilustração magnífica desta afirmação é a
solução, obtida por Gauss, para o problema da divisão da circunferência
em partes
iguais (RPM
4, p. 3).
Do ponto de
vista pedagógico, o tema tem ainda a vantagem de se constituir
em elemento importante na avaliação do aprendizado da Geometria em
geral.
Acreditamos
que esta nova seção poderá oferecer aos nossos colegas professores
e também aos estudantes um aspecto atraente e de alto valor educacional
da Matemática.
Paulo Leite
IME.USP
|
Uma construção geométrica e
a progressão geométrica |
Elon Lages
Lima
IMPA/CNPq.
Dados os
números reais a, r, com 0 < r < 1, seja S = a + ar + ar2
+
+ ... + arn +
...
a soma dos
termos da progressão geométrica ilimitada cujo
primeiro termo
é a e cuja razão é r. Temos:
S = a + r(a +
ar + ar2 + ...) = a + r
. S,
donde
S
 rS = a e daí rS = a e daí
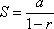
Não há
geometria alguma nesse raciocínio, embora a progressão se chame
geométrica.
Mas, dados a
> 0 e 0 < r < 1, podemos construir geometricamente a
soma S = a
+ ar + ar2 + ...
do seguinte modo:
Tomamos um
segmento de comprimento a e, a partir de uma de suas extremidades,
outro segmento, com um comprimento b arbitrário. Na outra extremidade,
traçamos um segmento paralelo a b, de comprimento rb.
A reta que
liga as extremidades livres dos segmentos b e rb encontra o
prolongamento de a num
ponto que dista exatamente S da primeira extremidade
de a.
A figura ao
lado diz mais do que as palavras acima.
 Explicação:
os
triângulos de bases
b e rb na figura ao lado são
semelhantes. A razão de semelhança é r. Logo ò segmento
adjacente a a mede rS. Ou seja, S
= Explicação:
os
triângulos de bases
b e rb na figura ao lado são
semelhantes. A razão de semelhança é r. Logo ò segmento
adjacente a a mede rS. Ou seja, S
=
= a + rS,
donde S = a/(l - r)
= a + ar +
ar2 + ...
Uma construção
análoga fornece um segmento de comprimento
S' = a
 ar + ar2
ar + ar2
 ar3
+ ... + (- l)narn + ...
ar3
+ ... + (- l)narn + ...
Neste
caso, temos
S' = a
 r(a
r(a
 ar + ar2 ar + ar2
 ar3 + ...), ar3 + ...),
ou seja,
S' = a
 rS' e daí S' = a/(1
+ r).
rS' e daí S' = a/(1
+ r).
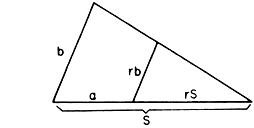
 A construção
de S' é dada na figura ao lado: A construção
de S' é dada na figura ao lado:
Os segmentos
b e rb são
paralelos,
traçados a partir das extremidades
do segmento a, porém
em sentidos opostos. Os dois
triângulos da figura são semelhantes
e a razão de semelhança é r.
Logo, se chamarmos S' a base
do triângulo maior, a base do
menor será r ■ S'. Portanto a =
S' + rS'
edaí
S' = a/(l + r) =
a
 ar + ar2
ar + ar2
 ar3
+ ...
ar3
+ ...
Wilson Massaro
Morro
Agudo, SP
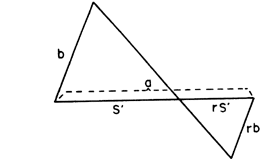
Incentro,
centro da circunferência inscrita em um triângulo, é o ponto de
encontro de
suas bissetrizes. Vejamos sua construção:
•
Centro em A
eraio AC, determina-se
o ponto D na reta AB.
 •
Centro em B
e raio BC, determina-se o ponto. E na
reta AB. •
Centro em B
e raio BC, determina-se o ponto. E na
reta AB.
•
Traça-se a
mediatriz de DE.
•
O ponto
médio, R, de DE é
o ponto
de tangência da circunferência inscrita.
•
Repete-se o
processo para um
outro
lado. O ponto de encontro
das
mediatrizes é o incentro do
triângulo.
Por que
funciona.
Se p
for o semiperímetro
do triângulo ABC, temos:
2x + 2y + 2z =
2p,
ou seja,
x+y+z=p.
Mas y + z
= a, logo, x = p-a.
O processo
acima é o da construção de um
ponto R
no lado AB do triângulo, tal que
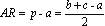 .
.
|
Determinação das coordenadas do incentro(*) |
Vamos
demonstrar que as coordenadas do incentro
I são:
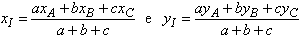
__________
(*) A
determinação das coordenadas do incentro é o problema 10 na RPM 2,
p. 32, proposto, na
ocasião, por
Wilson Massaro e Dermeval C. Neto. Duas soluções, da autoria de outros
colegas
foram
publicadas na RPM 3, p. 33. A solução, ora apresentada, oferece um
3.° caminho para
resolver a
problema.
 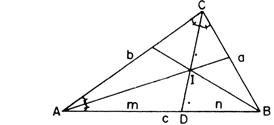 Demonstração: Demonstração:
Usaremos o
seguinte teorema:
A
bissetriz de um ângulo de um triângulo separa o lado oposto em segmentos, cujos comprimentos
são proporcionais aos comprimentos
dos lados adjacentes.
Aplicando o
teorema:
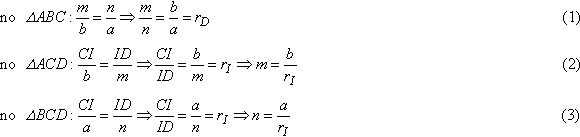
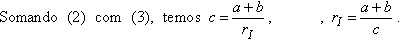
A Geometria
Analítica nos dá as coordenadas de um ponto P, entre A
e
B, que divide o segmento AB numa razão dada:
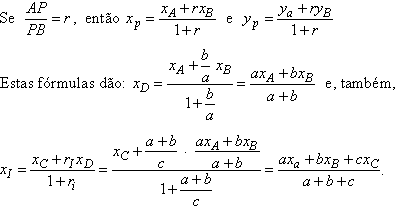
De modo análogo, obtém-se a expressão que dá yI.
|
 |
|
Wilson
Massaro
é licenciado
em Matemática pela FFCL "Barão
de Mauá" de Ribeirão Preto, SP e é professor da EEPSG "Manuel
Martins" de Morro Agudo, SP. |
|
 |
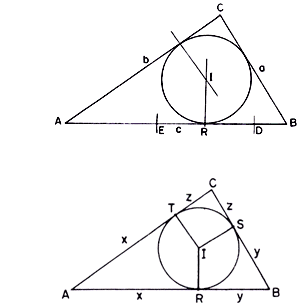
NR: O colega
Elio Mega, São Paulo, SP, descreveu o seguinte processo para
obter o incentro (usando
a notação da fig.2):
|