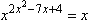
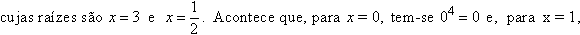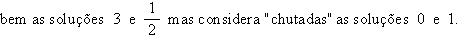
Um colega do Rio de Janeiro, RJ, coloca a seguinte questão: a equação exponencial se resolvida pela regra de "igualar os expoentes" nos leva a 2x2 7x + 4 =  1, tem-se  1-1 = 1,  o que mostra que x = 0 e x = 1  são também soluções do problema. O colega pergunta: como explicar isso a um aluno do 2.° grau? A experiência mostra que o aluno aceita   RPM: O colega percebeu que x =  1   também resolve o problema? Com efeito, E, então? Existirão, ainda, outras soluções? Esse é um dos perigos das regras prontas: deixam-nos completamente à deriva ao menor problema. Senão, vejamos como ter certeza de que estão esgotadas todas as possibilidades. A dificuldade aqui reside na definição de ab, quando a e b são números reais quaisquer. Ora, o que sabemos é que  ab  está definido sempre que: 1.  a é real positivo  (a > O)  e  b real qualquer, quando, então, se terá ab > 0 também; 2.  a = 0  e  b  real positivo  (b > 0),   quando  0b = 0; 3.  a é real negativo (a < 0) e b é um racional de forma irredutível  p/q, com  q  ímpar (q > 0),  quando ab = ().   No caso, então, da equação dada, em que o primeiro membro envolve uma potência de base real x,  é preciso separar os três casos, conforme x seja positivo, nulo ou negativo. 1.° caso: em que x > 0, logo ambos os membros da equação dada serão positivos, sendo possível tomar os seus logaritmos. Isto nos leva a (2x2 7x + 4)log x = log x (em qualquer base em que se considere o logaritmo). Esta última equação estará satisfeita se log x = 0 ou, se tivermos log x 0  e  2x2 7x + 4 = 1.   Aqui já aparecem as soluções x = 1,3  e   1/2. Certo? 2.° caso: em que x = 0. Então 2x2 7x + 4 assume o valor 4, o que dá ao primeiro membro da equação primitiva o valor  04 = 0,   donde x = 0  é, também, uma solução. 3.° caso: em que x < 0, quando, então, só sabemos calcular 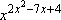quando o expoente for um racional com denominador ímpar. Seja, então,   2x2 7x + 4 = p/q na forma irredutível (isto é, p e q são primos entre si e q é ímpar). Repare que isto não acontece para todos os valores negativos de x, mas se pretendemos que esse valor seja solução da equação dada, devemos poder calcular xp/q e esse valor deve coincidir com x. Em particular xp/q deve ser negativo, o que força o número p a ser ímpar também. Consideremos, então, só os valores negativos de x para os quais 2x2 7x + 4 seja um racional p/q com p e q ímpares. Ora, se ainda. xp/q = x  tem.se xp = xq ou xp = xq ou (x)p = (x)q, dado que p e q são ímpares. Agora, estamos com potências de bases positivas e podemos tomar seus logaritmos (em qualquer base), obtendo-se plog(x) = q log(x). Esta equação admite as soluções log(x) = 0 e, portanto, x= 1  (é preciso, ainda, verificar se, para  x =  1, 2x2 - 7x + 4   é um racional  p/q  com  p  e q  ímpares. Isso é verdade  porque para   x =   1,  2x2 -  7x +  4 =  13)   ou,   se   log(x) 0,   p =  q  ímpar, donde  p/q = 1,   mas estamos com   x <  0   e   o estudo da parábola   2x2 7x + 4   mostra que p/q = 2x2 7x + 4 > 4  para x < 0,  logo não há outras soluções para o problema dado. É convincente?   Balcão do mestre Às Escolas Professor de Matemática licenciado pelo IME-USP, formado em Pedagogia pela FEUSP, procura escola para lecionar no 1? e/ou 2? graus. Aceita trabalhar fora de São Paulo. Paul William Dixon Rua Duzolina Gracioli Eleno, 43 Interlagos 04811 — São Paulo — SP Quem tem? Abecedário da Álgebra, Darcy Leal de Menezes — vol. 1 Curso de Álgebra, Sinézio de Farias — vol. 1 e que queira vender ou trocar Dirigir-se a Felizardo Toscano Rua Dom Bosco, 1329 Boa Vista 50070 — Recife — PE   Respostas dos probleminhas (p. 60) 1. 99 x 91;  2. 30 quadrados; 3. Não existe um caminho. (Pense nos quadrados como os de um tabuleiro de xadrês. João está, por exemplo, em um quadrado preto. Ao sair, entrará necessariamente em um quadrado branco, daí irá para um preto e assim por diante. Sua trajetória será preto, branco, preto, branco, ... preto, branco. Portanto não poderá terminar em   B,  que é preto.)