O problema do relógio
Resolução simplificada de um problema angular

Antonio Leonardo P. Pastor

São Paulo, SP Um resultado interessante que os alunos usam, e nem sempre sabem justificar, é o seguinte:

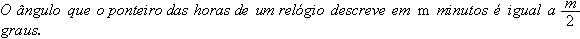
Consideremos, por exemplo, o problema: Calcular o ângulo formado pelos ponteiros de um relógio que marca 5 h 43 mim.

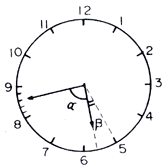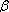É usual resolvermos assim: Seja o ângulo que o ponteiro das horas descreveu desde as 5 horas até 5 h 43 min. Ora, o mostrador do relógio é dividido em 12 partes iguais de 30° cada. Cada setor de 30° corresponde a 5 minutos e portanto cada minuto corresponde a 6^o. Assim, o ângulo a + 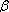pode ser determinado por contagem direta, e é igual a   18 ^. 6 =  108°.

É fácil verificar que o ângulo 0 é diretamente proporcional ao número m de minutos transcorridos, isto é, 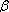= km (v. RPM 8, p., 3, Definição 1). Ora, sabemos que em uma hora o ângulo 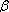descrito pelo' ponteiro menor é igual a 30°. Então:

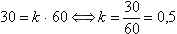
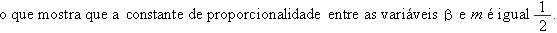
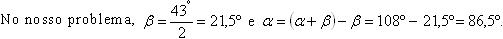
Em geral, tomando inicialmente a medida do ângulo que vai da marca da hora em questão até a marca do minuto correspondente, devemos somar ou subtrair o ângulo 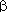(ângulo que o ponteiro das horas descreve durante os minutos correspondentes), dependendo do ângulo que o problema pede (maior ou menor), da configuração dos ponteiros e de como efetuamos a medição (orientação). Em resumo, a resolução de problemas simples como o do exemplo se reduz à determinação de  .

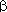Não quero aqui defender o uso de regras (pelo contrário!). Gostaria apenas de observar que a apresentação de uma regra simplificadora, que neste caso nada mais é do que uma conseqüência das proporções envolvidas, pode ser válida se o professor utilizá-la com o objetivo de motivar sua aula.

O leitor interessado encontrará outros problemas sobre razões e proporções, abordados sob um enfoque bastante atual, nos artigos do Professor Geraldo Ávila (RPM 8 e 9) e considerações adicionais no artigo do Professor Elon Lages Lima (RPM 9).

Como calcular valores aproximados de

Milton de Paula Garcia Ourinhos, SP

É comum, no 1º grau, principalmente na 8ª série, quando estudamos a área do círculo, perguntas como: — Professor, por que vale 3,14?

Após o estudo dos polígonos regulares, na 8? série, podemos, até como recreação, calcular valores aproximados de , sem grande trabalho, como veremos abaixo:

-.cja um polígono regular de  n  lados,   n 3,   cada lado medindo a.

Pelo Teorema dos Cossenos, temos:

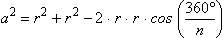
Observe que 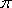não depende do raio de circunferência, já que r é eliminado na expressão acima.

Usando esta expressão, vamos calcular alguns valores aproximados de .
 

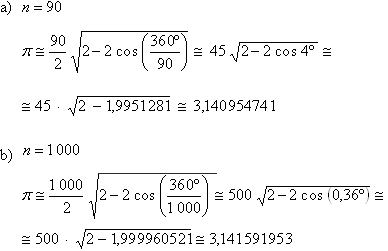
Observação. O fato de precisar usar uma calculadora para obter valores aproximados de não tira o objetivo deste artigo, que é mostrar que 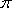é aproximadamente 3,14 e não depende do "tamanho" do círculo.