|
A
precisão do furo cilíndrico |
Luiz Márcio Imenes
FUNBEC |
|
Sérgio Roberto Nobe foi meu aluno há cerca de
15 anos. Hoje é professor da UNESP, em Rio Claro. Enquanto fazia o
curso de Matemática na UNICAMP, foi professor nos cursos técnicos do
SENAI. Certa vez, descreveu-me um processo, usado pêlos técnicos de
uma indústria, para verificar a precisão de um furo cilíndrico praticado
numa peça.
|

|
|
|
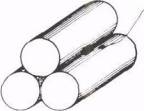 solda solda |
Já
não me lembro de certos detalhes. Vou resumir o relato, ignorando
alguns aspectos técnicos.
Consideremos três bastões cilíndricos, metálicos,
de mesmo raio r. Este raio deve ter uma medida conveniente,
como veremos seguir. Os três cilindros são fixados uns aos
outros (com solda, p exemplo), formando um conjunto solidário.
|
O
raio r deve ser calculado de modo que, ao introduzir este
conjunto no furo cilíndrico, os três bastões se ajustem sem
folga.
Girando o conjunto percebemos se o furo
praticado na peça é, de fato cilíndrico. Ele deve girar
"sem pegar" e sem folga.
|
 |
Pois
bem, a execução deste processo exige a solução de um problema de
Geometria. Na figura seguinte, os três círculos menores têm mesmo
raio r, são tangentes entre si dois a dois e cada um deles é
tangente ao círculo maior de raio R.
Devemos
calcular r em função de R.
Vamos
resolver o problema.
O
triângulo ABC é equilátero e seu lado é igual a 2r.
O ponto D é seu baricentro, logo

O
valor aproximado de  deve ser calculado considerando-se a precisão dos
instrumentos de medida usados na indústria. Se, por exemplo,
trabalhamos
com décimos de milímetro e R =
10,00 cm, deveremos ter:
deve ser calculado considerando-se a precisão dos
instrumentos de medida usados na indústria. Se, por exemplo,
trabalhamos
com décimos de milímetro e R =
10,00 cm, deveremos ter:
r = 0,464
x R =
4,64 cm.
|
Trigonometria na oficina mecânica.
|
Pedro Firmino
da Silva
São Roque, SP
|
Este
problema foi-me apresentado por um torneiro mecânico, que desejava
fazer 6 furos na base de uma peça de forma cilíndrica. A peça
ficaria assim:
O diâmetro da base media 120 mm e os
furos deveriam distribuir-se igualmente sobre uma circunferência
imaginária de diâmetro 100 mm.
|

|
|

barra milimetrada fixada à peça
|
Este problema pode ser resolvido graficamente
com muita simplicidade, usando-se um compasso. Entretanto, o
torneiro dispunha apenas de um outro instrumento que ele chamou de
altímetro. Vou apresentá-lo esquematicamente. Ele é
constituído por uma barra milimetrada e uma régua que desliza
perpendicularmene à barra. Esta é fixada à peça.
Para resolver o problema, primeiro desenhamos, com a régua
móvel,
um diâmetro da base.
|
|
 |
Sobre ele marcamos os centros
dos dois
primeiros furos, que ficarão afastados de 100 mm.
Imaginaremos o problema resolvido. Seja r
a reta que contém o diâmetro.
Com a divisão da circunferência em 6 partes
iguais, obtemos ângulos centrais de 60°. As retas s e t
são paralelas à reta r e suas distâncias a ela são iguais a
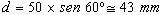
|
|
Deste modo, com a régua móvel, desenhamos
as retas s e t, sobre
as quais
estarão
os outros quatro furos. |
|
A régua móvel, sempre perpendicular à barra fixa, executa um
movimento de translação. Como não é possível transladar a barra
(que é fixa), giramos o altímetro de 90°, colocando a barra sobre
o diâmetro desenhado.
Outra vez, imaginamos o problema resolvido.
A distância e é dada por:
e =
50 . sen 30° =
25 mm
Assim,
deslocando a régua móvel, marcamos os centros dos outros quatro furos.
|

|
|